Содержание водяных паров[править]
Абсолютной влажностью воздуха называется количество водяного пара в г, содержащегося в 1 м3 воздуха. Абсолютная влажность измеряется количеством водяного пара во влажном воздухе (ϒn — г/м3).
Таблица 6.2. Абсолютная влажность насыщенного воздуха при разных температурах
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
||
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
Влагосодержание воздуха – это масса водяных паров в граммах (W), содержащихся в смеси, отнесенное к массе сухого воздуха в кг. Влагосодержание (d) определяется из соотношения\ , г/кг
или через соответствующие парциальные давления водяных паров Рп и сухой части воздуха Рв\, г/кг
или
\(d=622*\frac{P_п}{P_н-P_п}\), г/кг
где: Рн = Рп + Рв .
Влагоемкостью называется влагосодержание 1 кг воздуха в насыщенном состоянии, выраженное через парциальные давления\ , г/кг
Относительная влажность воздуха (степень насыщения влагой) – это отношение абсолютной влажности данного (ненасыщенного) воздуха к абсолютной влажности насыщенного воздуха при той же температуре:
ϕ = γn / γн * 100, %
или отношение парциального давления водяных паров в воздухе к парциальному давлению (Рн) водяных паров при той же температуре и полном насыщении воздуха:
ϕ = Pn / Pн * 100, %
Температурой точки росы называется наинизшая температура, до которой можно охлаждать воздух при постоянном влагосодержании. Дальнейшее понижение температуры вызывает конденсацию.
Таблица 6.3. Объем влажного воздуха на 1 кг сухого при Р=99,3 кПа (745 мм рт.ст.) (Vм3/кг сухого воздуха)
| t°C | |
|||||||
| 100 | 90 | 80 | 70 | 60 | 50 | 40 | 30 | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
Таблица 6.4. Физические свойства насыщенного воздуха при атмосферном давлении Рн=101,325 кПа (760 мм рт. ст.)
| |
Плотность насыщенного воздуха, ρ, кг/м3 |
|
Количество водяных паров, содержащихся в 1кг насыщенного воздуха – d, г | t °C | Плотность насыщенного воздуха – ρ, кг/м3 |
Парциальное давление насыщающих водяных паров – (мм рт. ст.) |
Количество водяных паров, содержащихся в 1кг насыщенного воздуха – d, г |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
Задача №1 на расчет количества теплоты
Рассчитайте количество теплоты, необходимое для нагрева $15 \space кг$ меди на $80 \degree C$.
Дано:$m = 15 \space кг$$c = 400 \frac{Дж}{кг \cdot \degree C}$$\Delta t = 80 \degree C$
$Q — ?$
Показать решение и ответ
Скрыть
Решение:
Для решения этой задачи мы будем использовать формулу для расчета количества теплоты, необходимого для нагревания тела:$Q = cm(t_2 — t_1)$.
В данном случае нам не известны начальная и конечная температуры тела ($t_2$ и $t_1$). Нам известно изменение этой температуры: $\Delta t = t_2 — t_1$. Тогда формула для расчета количества теплоты примет вид:$Q = cm \Delta t$.
Подставим значения всех величин и рассчитаем количество теплоты:$Q = 400 \frac{Дж}{кг \cdot \degree C} \cdot 15 \space кг \cdot 80 \degree C = 480 \space 000 \space Дж = 480 \space кДж$.
Ответ: $Q = 480 \space кДж$.
Задача №6 на использование графика
Используя график зависимости температуры керосина от сообщенного ему количества теплоты (рисунок 1), определите массу керосина.
Рисунок 1. График зависимости температуры керосина от сообщаемого количества теплоты
Для начала нам нужно записать условия задачи. Из графика мы видим, что начальная температура керосина $t_1$ была равна $0 \degree C$. Теперь выберем удобную нам точку на графике. Например, когда керосину сообщили количество теплоты $Q$, равное $2 \space кДж$, его температура $t_2$ стала равной $10 \degree C$. Теперь мы можем записать условия задачи и решить ее. Удельная теплоемкость керосина известна нам из таблицы.
Дано:$Q = 2 \space кДж$ $t_1 = 0 \degree C$$t_2 = 10 \degree C$$c = 2100 \frac{Дж}{кг \cdot \degree C}$
СИ:$Q = 2 \cdot 10^3 \space Дж$
$m — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Формула для расчета количества теплоты, необходимого для нагревания тела:$Q = cm(t_2 — t_1)$.
Выразим отсюда массу:$m = \frac{Q}{c (t_2 — t_1)}$.
Рассчитаем ее:$m = \frac{2 \cdot 10^3 \space Дж}{2100 \frac{Дж}{кг \cdot \degree C} \cdot (10 \degree C — 0 \degree C)} \approx 0.095 \space кг \approx 100 \space г$.
Ответ: $m \approx 100 \space г$.
Задача №2 на расчет количества теплоты
Рассчитайте количество теплоты, необходимое, чтобы нагреть бассейн объемом $300 \space м^3$ на $10 \degree C$.
В задаче идет речь о бассейне, а значит, о пресной воде. Она имеет плотность, равную $1000 \frac{кг}{м^3}$. Запишем условия задачи и решим ее.
Дано:$V = 300 \space м^3$$\Delta t = 10 \degree C$$c = 4200 \frac{Дж}{кг \cdot \degree C}$$\rho = 1000 \frac{кг}{м^3}$$c = 4200 \frac{Дж}{кг \cdot \degree C}$
$Q — ?$
Показать решение и ответ
Скрыть
Решение:
Формула для расчета количества теплоты, необходимого для нагревания тела:$Q = cm(t_2 — t_1)$.
Нам неизвестна масса воды в бассейне, но известен ее объем и плотность. Плотность по определению:$\rho = \frac{m}{V}$.
Тогда масса будет равна:$m = \rho V$.
Также нам неизвестны начальная и конечная температуры тела ($t_2$ и $t_1$). Нам известно изменение этой температуры: $\Delta t = t_2 — t_1$. Тогда формула для расчета количества теплоты примет вид:$Q = c \rho V \Delta t$.
Рассчитаем количество теплоты:$Q = 4200 \frac{Дж}{кг \cdot \degree C} \cdot 1000 \frac{кг}{м^3} \cdot 300 \space м^3 \cdot 10 \degree C = 12.6 \cdot 10^9 \space Дж = 12.6 \space ГДж$.
Ответ: $Q = 12.6 \space ГДж$.
Задача №3 на расчет массы
Найдите массу глицерина, если при нагревании от $10 \degree C$ до $15 \degree C$ он поглотил $12 \space кДж$ теплоты. Удельная теплоемкость глицерина равна $2430 \frac{Дж}{кг \cdot \degree C}$.
Дано:$Q = 12 \space кДж$ $t_1 = 10 \degree C$$t_2 = 15 \degree C$$c = 2430 \frac{Дж}{кг \cdot \degree C}$
СИ:$Q = 12 \cdot 10^3 \space Дж$
$m — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Формула для расчета количества теплоты, необходимого для нагревания тела:$Q = cm(t_2 — t_1)$.
Выразим отсюда массу глицерина:$m = \frac{Q}{c(t_2 — t_1)}$.
Рассчитаем:$m = \frac{12 \cdot 10^3 \space Дж}{2430 \frac{Дж}{кг \cdot \degree C} \cdot (15 \degree C — 10 \degree C)} \approx 1 \space кг$.
Ответ: $m \approx 1 \space кг$.
Задача №5 на расчет удельной теплоемкости
В калориметр было налито $450 \space г$ воды, температура которой $20 \degree C$. Когда в эту воду погрузили $200 \space г$ железных опилок, нагретых до $100 \degree C$, температура воды стала равна $24 \degree C$. Определите удельную теплоемкость опилок.
Записывая условия задачи, используем индекс “в” для обозначения величин, связанных с водой, и индекс “ж” для обозначения величин, связанных с железными опилками.
Дано:$m_в = 450 \space г$$m_ж = 200 \space г$ $t_{в1} = 20 \degree C$$t_{в2} = 24 \degree C$$c_в = 4200 \frac{Дж}{кг \cdot \degree C}$$t_{ж1} = 100 \degree C$
СИ: $m_в = 0.45 \space кг$$m_ж = 0.2 \space кг$
$с_ж — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Формула для расчета количества теплоты, необходимого для нагревания тела и выделяемого при его охлаждении:$Q = cm(t_2 — t_1)$.
Запишем эту формулу для воды:$Q_в = c_в m_в (t_{в2} — t_{в1})$.
Запишем формулу количества теплоты для железных опилок:$Q_ж = c_ж m_ж (t_{ж2} — t_{ж1})$.
Нагретые железные опилки помещают в воду для их охлаждения. Значит, вода будет нагреваться и поглотит некоторое количество теплоты, а опилки будут охлаждаться и выделят некоторое количество теплоты. Т.е., между этими телами будет происходить теплообмен, для которого действует уже известное вам правило:
Это значит, что количество теплоты $Q_в$, полученное водой, будет равно количеству теплоту $Q_ж$, которое выделится при охлаждении железных опилок, но с обратным знаком: $Q_в = — Q_ж$.
Подставим выражения, которые дает формула для расчета количества теплоты:$c_в m_в (t_{в2} — t_{в1}) = — c_ж m_ж (t_{ж2} — t_{ж1})$.
После завершения теплообмена температура воды и температура железных опилок будут равны друг другу: $t_в2 = t_ж2 = t_2$.
Подставим в наше равенство и выразим $c_ж$:$c_ж = — \frac{c_в m_в (t_2 — t_{в1})}{m_ж (t_2 — t_{ж1})}$.
Рассчитаем удельную теплоемкость железных опилок:$c_ж = — \frac{4200 \frac{Дж}{кг \cdot \degree C} \cdot 0.45 \space кг \cdot (24 \degree C — 20 \degree C)}{0.2 \space кг \cdot (24 \degree C — 100 \degree C)} = — \frac{7560 \space Дж}{- 15.2 \space кг \cdot \degree C} \approx 497 \frac{Дж}{кг \cdot \degree C} \approx 0.5 \frac{кДж}{кг \cdot \degree C}$.
Ответ: $c_ж \approx 0.5 \frac{кДж}{кг \cdot \degree C}$.
Закон Гесса

На основе широких и систематических исследований химических реакций, сопровождающихся выделением или поглощением теплоты, Г. Гесс сформулировал такой закон:
тепловой эффект химической реакции не зависит от пути её протекания, а зависит только от природы и агрегатного состояния (твердого, жидкого, газообразного) исходных веществ и продуктов реакции.
Другими словами, тепловой эффект любой химической реакции не зависит от того, образовалось ли соединение сразу из исходных веществ, или его образование произошло вследствие течения ряда последовательных реакций. Это можно объяснить на примере превращения углерода (графита) в карбон(IV) оксид:

Все указанные реакции происходят с выделением теплоты, то есть являются экзотермическими. Согласно закону Гесса:
∆Н1+∆Н2=∆Н,
-110,5 кДж-285,5 кДж = -396 кДж.
Задача №7 на расчет температуры нагрева
Стальной резец массой $2 \space кг$ был нагрет до температуры $800 \degree C$ и затем опущен в сосуд, содержащий $15 \space л$ воды при температуре $10 \degree C$. До какой температуры нагреется вода в сосуде?
Записывая условия задачи, используем индекс “в” для обозначения величин, связанных с водой, и индекс “р” для обозначения величин, связанных со стальным резцом.
Дано:$V_в = 15 \space л$ $m_р = 2 \space кг$$t_{р1} = 800 \degree C$$c_р = 500 \frac{Дж}{кг \cdot \degree C}$$\rho_в = 1000 \frac{кг}{м^3}$$c_в = 4200 \frac{Дж}{кг \cdot \degree C}$$t_{в1} = 10 \degree C$
СИ:$V_в = 15 \cdot 10^3 м^3$
$t_{в2} — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Когда нагретый резец опускают в холодную воду, между этими двумя телами происходит теплообмен. Резец остывает и выделяет энергию, а вода получает эту энергию и нагревается. Соответственно, количество теплоты, которое выделится при остывании стального резца, численно будет равно количеству теплоту, которое получит вода.
Когда теплообмен завершится,температуры стального резца и воды будут одинаковы: $t_{в2} = t_{р2} = t_2$.
Запишем формулу для расчета количества теплоты, которое выделится при остывании резца:$Q_р = с_р m_р (t_2 — t_{р1})$.
Запишем формулу для расчета количества теплоты, которое получила вода:$Q_в = с_в m_в (t_2 — t_{в1})$.
Приравняем правые части этих уравнений, не забыв про знак “минус”, которые указывает на выделение энергии при охлаждении тела:$с_р m_р (t_2 — t_{р1}) = — с_в m_в (t_2 — t_{в1})$.
Раскроем скобки:$с_р m_р t_2 — с_р m_р t_{р1} = — с_в m_в t_2 + с_в m_в t_{в1}$.
Перенесем множители с $t_2$ на одну сторону уравнения и выразим эту температуру, до которой нагреется вода:$с_р m_р t_2 + с_в m_в t_2 = с_в m_в t_{в1} + с_р m_р t_{р1}$,$t_2 (с_р m_р + с_в m_в) = с_в m_в t_{в1} + с_р m_р t_{р1}$,$t_2 = \frac{с_в m_в t_{в1} + с_р m_р t_{р1}}{с_р m_р + с_в m_в}$.
Нам неизвестна масса воды, но известны ее плотность и объем. Выразим и рассчитаем массу через эти величины:$m_в = \rho_в V_в = 1000 \frac{кг}{м^3} \cdot 15 \cdot 10^3 м^3 = 15 \space кг$.
Теперь мы можем рассчитать температуру $t_2$:$t_2 = \frac{4200 \frac{Дж}{кг \cdot \degree C} \cdot 15 \space кг \cdot 10 \degree C + 500 \frac{Дж}{кг \cdot \degree C} \cdot 2 \space кг \cdot 800 \degree C}{500 \frac{Дж}{кг \cdot \degree C} \cdot 2 \space кг + 4200 \frac{Дж}{кг \cdot \degree C} \cdot 15 \space кг} = \frac{630 \cdot 10^3 \space Дж + 800 \cdot 10^3 \space Дж}{1 \cdot 10^3 \frac{Дж}{\degree C} + 63 cdot 10^3 \frac{Дж}{\degree C}} = \frac{1430 \cdot 10^3 \space Дж}{64 \cdot 10^3 \frac{Дж}{\degree C}} \approx 22.3 \degree C$.
Ответ: $t_2 \approx 22.3 \degree C$.
Гигакалории или киловатты
Разберемся окончательно, в чем отличие этих единиц измерения. Пусть у нас имеется нагревательный прибор, например, чайник. Возьмем 1 литр холодной воды из-под крана (температура t1=15°C) и вскипятим ее (нагреем до температуры t2=100°C). Электрическая мощность чайника — P=1,5 кВт. Сколько тепла поглотит вода? Чтобы это узнать, применим знакомую нам формулу, при этом учтя, что масса 1 литра воды m=1 кг: Q=4183 [Дж/(кг*°C)]*1 кг*(100°С-15°С)=355555 Дж=84922,8528 кал≈85 ккал.
За какое время вскипит чайник? Пусть вся энергия электрического тока уйдет на нагрев воды. Тогда неизвестное время мы найдем, используя энергетический баланс: «Энергия, расходуемая чайником, равна энергии, поглощаемой водой (без учета потерь)». Энергия, расходуемая чайником за время τ, равна P*τ. Энергия, поглощаемая водой, равна Q. Тогда на основе баланса получим P*τ=Q. Отсюда время нагрева чайника составит: τ=Q/P=355555 Дж/1500 Вт≈237 с≈4 мин. Количество теплоты, переданное чайником воде за единицу времени — это и есть его тепловая мощность. Она составит в нашем случае величину Q/τ=84922,8528 кал/237 с≈358 кал/с=0,0012888 Гкал/ч.
Таким образом, кВт и Гкал/ч — это единицы мощности, а Гкал и МДж — единицы теплоты и энергии. Как подобные расчеты можно применить на практике? Если нам приходит квитанция об оплате отопления, то мы платим за тепло, которое снабжающая организация поставляет нам по трубам. Это тепло учитывается в гигакалориях, т. е. в количестве теплоты, потребленном нами за расчетный период. Нужно ли переводить эту единицу в джоули? Конечно, нет, потому что мы просто платим за конкретное число гигакалорий.
Однако часто бывает необходимо выбрать для дома или квартиры те или иные отопительные приборы, например, кондиционер, радиатор, бойлер или газовый котел. В связи с чем требуется заранее знать тепловую мощность, требуемую для обогрева помещения. Зная эту мощность, можно подобрать соответствующий прибор. Она может быть указана как в кВт, так и в Гкал/ч, а также в единицах BTU/h (British Thermal Unit — Британская Термическая Единица, h — час). Следующая памятка поможет вам перевести кВт в Гкал/ч, кВт в BTU/h, Гкал в кВт*ч и BTU в кВт*ч.
Памятка 2
- один Вт=одному Дж/с=0,2388459 кал/с=859,8452 кал/ч=0,8598 ккал/ч;
- один кВт=одному кДж/с=1000 Дж/с=238,8459 кал/с=859845,2279 кал/ч=0,00085984523 Гкал/ч;
- один МВт=один МДж/с=один млн Дж/с=1000 кВт=238845,8966 кал/с=0,85984523 Гкал/ч;
- одна Гкал/ч=один млрд кал/ч=1163000 Вт=1163 кВт=1,163 МВт=3968156 BTU/h;
- одна BTU/h=0,2931 Вт=0,0700017 кал/с=252,0062 кал/ч=0,2520062 ккал/ч;
- один Вт=3,412 BTU/h, один кВт=3412 BTU/h, один МВт=3412000 BTU/h.
Как определяется единица BTU/h и для чего она используется? 1 BTU — это количество теплоты, необходимое для нагревания 1 фунта воды на 1° по Фаренгейту (°F). Эта единица измерения используется в основном для обозначения тепловой мощности установок, таких, например, как кондиционеры.
Задача №8 на смешивание трех жидкостей
Какой температуры получится вода, если смешать $0.02 \space кг$ воды при $15 \degree C$, $0.03 \space кг$ воды при $25 \degree C$ и $0.01 \space кг$ воды при $60 \degree C$?
Дано:$m_1 = 0.02 \space кг$$t_1 = 15 \degree C$$m_2 = 0.03 \space кг$$t_2 = 25 \degree C$$m_3 = 0.01 \space кг$$t_3 = 60 \degree C$
$t — ?$
Посмотреть решение и ответ
Скрыть
Решение:
При смешивании жидкостей разных температур, мы знаем, что внутренняя энергия всех нагревающихся тел увеличивается на столько, на сколько уменьшается внутренняя энергия остывающих тел.
Для смешивания двух жидкостей мы можем записать, что $Q_1 = — Q_2$ или $Q_1 + Q_2 = 0$.
Сначала рассмотрим смешивание первых двух порций воды. Первая порция с температурой $15 \degree C$ будет нагреваться (получать энергию), а вторая порция с температурой $25 degree C$ будет охлаждаться (выделять энергию). Эти энергии будут численно равны друг другу, но противоположны по знаку:$cm_1(t_{1+2} — t_1) = — cm_2(t_{1+2} — t_2)$.
Найдем конечную температуру этой смеси:$m_1(t_{1+2} — t_1) = — m_2 (t_{1+2} — t_2)$,$m_1 t_{1+2} — m_1 t_1 = -m_2 t_{1+2} + m_2 t_2$,$t_{1+2} (m_1 + m_2) = m_1 t_1 + m_2 t_2$,
$t_{1+2} = \frac{m_1 t_1 + m_2 t_2}{m_1 + m_2} = \frac{0.02 \space кг \cdot 15 \degree C + 0.03 \space кг \cdot 25 \degree }{0.02 \space кг + 0.03 \space кг} = \frac{0.3 \space кг \cdot \degree + 0.75 \space кг \cdot \degree C}{0.05 \space кг} = 21 \degree C$.
Так мы получили смесь первой и второй порций воды массой $m_{1+2} = 0.05 \space кг$ и температурой $t_{1+2} = 21 \degree C$.
Теперь добавим третью порцию воды в полученную смесь. Смесь будет нагреваться (получать энергию), а третья порция воды будет охлаждаться (выделять энергию):$Q_{1+2} = — Q_3$.$cm_{1+2} (t — t_{1+2}) = — cm_3 (t — t_3)$,$m_{1+2} (t — t_{1+2}) = — m_3 (t — t_3)$.
Выразим отсюда конечную температуру смеси из трех порций воды $t$:$m_{1+2} t — m_{1+2} t_{1+2} = -m_3 t + m_3 t_3$,$t (m_{1+2} + m_3) = m_{1+2} t_{1+2} + m_3 t_3$,$t = \frac{m_{1+2} t_{1+2} + m_3 t_3}{m_{1+2} + m_3}$.
Рассчитаем ее:$t = \frac{0.05 \space кг \cdot 21 \degree C + 0.01 \space кг \cdot 60 \degree}{0.05 \space кг + 0.01 \space кг} = \frac{1.05 \space кг \cdot \degree C + 0.6 \space кг \cdot degree C}{0.06 \space кг} = 27.5 \degree C$.
Ответ: $t = 27.5 \degree C$.
Задача №4 на расчет плотности
Определите плотность машинного масла объемом $1 \space л$, если известно, что для увеличения температуры на $30 \degree C$ ему требуется передать $45 \space кДж$ теплоты. Удельная теплоемкость масла равна $1.67 \frac{кДж}{кг \cdot \degree C}$.
Дано:$V = 1 \space л$$Q = 45 \space кДж$$c = 1.67 \frac{кДж}{кг \cdot \degree C}$$\Delta t = 30 \degree C$
СИ:$V = 10^{-3} \space м^3$$Q = 45 \cdot 10^3 \space Дж$$c = 1.67 \cdot 10^3 \frac{Дж}{кг \cdot \degree C}$
$\rho — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Формула для расчета количества теплоты, необходимого для нагревания тела:$Q = cm(t_2 — t_1)$.
Нам известны изменение температуры ($\Delta t = t_2 — t_1$), количество теплоты и удельная теплоемкость машинного масла. Выразим массу и рассчитаем ее:$m = \frac{Q}{c \Delta t} = \frac{45 \cdot 10^3 \space Дж}{1.67 \cdot 10^3 \frac{Дж}{кг \cdot \degree C} \cdot 30 \degree C} \approx 0.9 \space кг$.
По определению плотности:$\rho = \frac{m}{V}$.
Рассчитаем плотность машинного масла:$\rho = \frac{0.9 \space кг}{10^{-3} \space м^3} = 0.9 \cdot 10^3 \frac{кг}{м^3} = 900 \frac{кг}{м^3}$.
Ответ: $\rho = 900 \frac{кг}{м^3}$.
Что такое калория
Калория была введена еще в 1772 году шведским физиком-экспериментатором Иоганном Вильке в качестве единицы измерения теплоты. В настоящее время единица, кратная калории — гигакалория (Гкал), активно применяется в таких сферах жизнедеятельности, как коммунальное хозяйство, системы отопления и теплоэнергетика. Также используется ее производная — гигакалория в час (Гкал/ч), характеризующая скорость тепловыделения или теплопоглощения тем или иным оборудованием. Попробуем теперь рассчитать, чему равна одна калория.
Еще в школе на уроках физики нас учили, что для нагрева любого вещества ему необходимо сообщить определенное количество теплоты. Была даже такая формула Q=c*m*∆t, где Q означает неизвестное количество теплоты, m — массу нагреваемого вещества, c — удельную теплоемкость этого вещества, а ∆t — разность температур, на которую нагревают вещество. Так вот, калорией называют внесистемную единицу количества теплоты, определяемую как «количество теплоты, затрачиваемое на нагревание 1 грамма воды на 1 градус Цельсия при атмосферном давлении 101325 Па».
Поскольку теплота измеряется в джоулях, то используя вышеприведенную формулу, мы узнаем, чему равна 1 калория (кал) в джоулях. Для этого возьмем из справочника по физике значение удельной теплоемкости воды при нормальных условиях (атмосферное давление р=101325 Па, температура t=20°C): с=4183 Дж/(кг*°С). Тогда одна калория будет равна:
1 кал=4183 [Дж/(кг*°С)]*0,001 кг*1°С=4,183 Дж.
Однако величина калории зависит от температуры нагревания, поэтому ее значение не постоянно. Для практических же целей используется так называемая калория международная или просто калория, которая равна 4,1868 Дж.
Памятка 1
- 1 кал=4,1868 Дж, 1 ккал=1000 кал, 1 Гкал=1 млрд кал=4186800000 Дж=4186,8 МДж;
- 1 Дж=0,2388 кал, 1 МДж=1 млн. Дж=238845,8966 кал=238,8459 ккал;
- 1 Гкал/ч=277777,7778 кал/с=277,7778 ккал/с=1163000 Дж/с=1,163 МДж/с.
Задача №9 на расчет количества теплоты, рассеиваемого в окружающую среду
Электрочайник с водой нагревается от температуры $70 \degree C$ до температуры $80 \degree C$ за $3 \space мин$, а остывает от температуры $80 \degree C$ до температуры $70 \degree C$ за $9 \space мин$. Какая часть количества теплоты, выделяемой спиралью чайника при нагревании воды, рассеивается в окружающую среду? Тепловые потери считать постоянными.
Внесем необходимые пояснения. Спираль чайника передает воде определенное количество теплоты $Q_2$. Часть ее ($Q_1$) рассеивается в окружающую среду. Т.е., количество теплоты $Q_2$, выделяемое спиралью, больше количества теплоты $Q$, необходимого для нагрева воды.
Дано:$t_1 = 70 \degree C$$t_2 = 80 \degree C$$T_1 = 3 \space мин$$T_2 = 9 \space мин$
$\frac{Q_1}{Q_2} — ?$
Показать решение и ответ
Скрыть
Решение:
Сначала рассчитаем количество теплоты, которое необходимо сообщить воде в чайнике, чтобы ее температура увеличилась с $70 \degree C$ до $80 \degree C$:$Q = cm(t_2 — t_1)$.
Масса воды в чайнике нам неизвестна, поэтому примем ее, равной $1 \space кг$. Тогда,$Q = 4200 \frac{Дж}{кг \cdot \degree C} \cdot 1 \space кг \cdot (80 \degree C — 70 \degree C) = 42 \space 000 \space Дж = 42 \space кДж$.
Когда вода в чайнике остывает с температуры $80 \degree C$ до температуры $70 \degree C$, она выделяет в окружающую среду точно такое же количество энергии $Q$. Остывание происходит за $9 \space мин$. Значит, количество теплоты, которое выделяется в окружающую среду за $1 \space мин$ будет равно:$Q_0 = \frac{42 \space кДж}{9 \space мин} \approx 4.7 \frac{кДж}{мин}$.
В условиях задачи сказано, что тепловые потери постоянны. Это означает, что вода массой $1 \space кг$ отдает $4.7 \space кДж$ каждую минуту, в том числе, и при ее нагревании.
Нагревается вода за 3 минуты. За это время она отдает в окружающую среду следующее количество теплоты:$Q_1 = 4.7 \space кДж \cdot 3 = 14.1 \space кДж$.
Тем не менее, чайник нагрел воду до нужной температуры. Значит, он сообщил воде количество энергии, равное $Q_2 = Q + Q_1$.$Q_2 = 42 \space кДж + 14.1 \space кДж = 56.1 \space кДж$.
Теперь мы можем рассчитать отношение $\frac{Q_1}{Q_2}$, и узнать какая часть теплоты, выделяемая спиралью чайника, рассеивается в окружающую среду:$\frac{Q_1}{Q_2} = \frac{14.1 \space кДж}{56.1 \space кДж} \approx 0.25$.
Т.е., в окружающую среду рассеивается $\frac{1}{4}$ часть энергии, сообщаемая воде в чайнике.
Можно доказать, что это соотношение останется постоянным для воды любой массы в этой задаче. Чем больше будет масса воды, тем больше энергии ей будет нужно, чтобы нагреться до определенной температуры. Больше будут и тепловые потери. Искомое соотношение же останется неизменным.
Ответ: $\frac{Q_1}{Q_2} \approx 0.25$.
Тепловой эффект химической реакции
Любая химическая реакция зависит от разрыва одних химических связей и образования других. Когда в результате химической реакции при образовании новых связей выделяется энергии больше, чем требовалось для разрушения «старых» связей в исходных веществах, то избыток энергии выделяется как тепло. Примером могут служить реакции горения. Например, природный газ (метан CH₄) сгорает в кислороде воздуха с выделением большого количества теплоты.
Реакции, протекающие с выделением теплоты, называются экзотермическими. Если реакция экзотермическая, то содержание энергии в исходных реагентах больше, чем в продуктах реакции. Теплота выделяется в окружающую среду и энергия реакционной системы уменьшается, тогда тепловой эффект будет отрицательным.
В другом случае, если реакция протекает с поглощением теплоты, то такая реакция называется эндотермической. Для эндотермических реакций содержание энергии в исходных реагентах меньше, чем в продуктах реакции. Теплота поступает в систему, энергия системы увеличивается, тепловой эффект H будет положительным.
Тепловой эффект реакции ΔH (энтальпия) – это разница между содержанием энергии в исходных реагентах и конечных продуктах реакции.
Тепловой эффект реакции записывают отдельно от химического уравнения.
2Mg+O2=2MgO;
∆Н= -1250 кДж.
Тепловой эффект реакции определяют для вещества количеством 1 моль, поэтому в термохимическом уравнении допускается и дробный коэффициент:
С+Н2О=СО+Н2;
∆Н=+131,4кДж.
Н2+0,5О2→Н2О+285,8кДж.
Расчеты по термохимическим уравнениям
Приведем несколько примеров термохимических расчётов.
Задача 1
При разложении 222 г кальция гидроксида поглощается 2955 кДж теплоты. Составьте термохимическое уравнение этой реакции.
Решение
- Записываем термохимическое уравнение реакции разложения Са(OH)₂: Са(ОН)2=СаО+Н2О
Данное уравнение соответствует разложению 1 моль Са(ОН)₂, то есть 74 г.
- Рассчитаем количество вещества Ca(OH)₂:
v(Cа(ОН)2)=(m(Ca(OH)2))/(M(Ca(OH)2))=222 г/74 г/моль = 3моль.
- Количество теплоты, что соответствует 1 моль Са(ОН)₂, определим по пропорции:
на разложение 3 моль Са(ОН)₂ потрачено 2955 кДж теплоты, а на разложение 1 моль Са(ОН)₂ – x кДж теплоты. Отсюда:
х=(1моль*2955КДж)/3моль=985кДж.
Термохимическое уравнение разложения Са(ОН)₂ имеет такой вид:
Задача 2
2С2Н2 (г)+5О2 (г) = 4СО2 (г)+2Н2О (р),
Са(ОН)2 = СаО + Н2О,
∆Н298 = 985 кДж.
Термохимическое уравнение сгорания ацетилена такое:
∆Н298 = -2520 кДж.
Сколько теплоты выделится в результате сгорания 5 л (н. у.) ацетилена?
Решение
Из термохимического уравнения реакции:
в результате сгорания 2 моль С₂Н₂, то есть 2 • 22,4 л, выделяется 2520 кДж теплоты, х = 5л*2520 кДж/44,8 л = 281,25 кДж
тогда в результате сгорания 5 л С₂Н₂ выделится x кДж теплоты. Отсюда
Ответ: 281,25 кДж.
Задача 3
Термохимическое уравнение реакции получения фосфор (V) оксида:
4Р(тв)+5О2(г)=2Р2О5(тв),
∆Н298= -2984 кДж
Рассчитайте массу фосфора и обьем кислорода (н. у.), которые вступили в реакцию, если при этом выделилось 746 кДж теплоты.
Решение
- Записываем термохимическое уравнение горения фосфора и подставляем данные:
- Вычисляем:
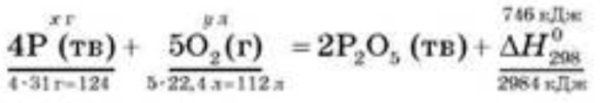
M(Р)=х=4*31 г*746кДж/2984 кДж = 31 г;
V(O2)=y=5*22,4 л*746 кДж/2984 кДж =28 л.
Ответ: 31 г; 28 л.
Термохимические уравнения
Область химии, занимающаяся изучением тепловых эффектов химических реакций, называется термохимией. Уравнения химических реакций, при которых приведен тепловой эффект, называют термохимическими уравнениями.
В термохимических уравнениях, в отличие от обычных химических уравнений, обязательно указывают агрегатные состояния веществ (жидкое «г.», твердое «тв.» или газообразное «г.»). Это связано с тем, что одно и то же вещество в разных агрегатных состояниях имеет разную энтальпию. Поэтому химическая реакция с участием одинаковых веществ, но в разном агрегатном состоянии, имеет разный тепловой эффект.
Тепловой эффект реакции в термохимических уравнениях обозначают двумя способами:
указывают только знак ΔΗ – если нужно указать, является ли реакция экзо- или эндотермической:
2Na(тв.)+2H2O(p.)=2NaOH(тв.)+H2(г.);
∆H<0.
СаСО3(тв.)=СаО(тв.)+СО2(г.);
∆H˃0.
указывают количественное значение – при необходимости проведения расчетов:
2Na(тв.)+2H2O(p.)=2NaOH(тв.)+H2(г.);
∆H=-281кДж/моль.
СаСО3(тв.)=СаО(тв.)+СО2(г.);
∆H=+177кДж/моль.
Изменение энтальпии, приведенное в термохимическом уравнении, – это та же часть химического уравнения, как и формулы веществ, и поэтому подчиняется тем же соотношениям. Например, для уравнения горения этана:
2C2H6(г.)+7O2(г.)=4СO2(г.)+6Н2O(p.)
∆H=3120 кДж/моль.


































